Descripción de un conjunto
Existen dos maneras de describir o especificar los elementos de un conjunto:
Una de ellas es mediante una definición intensiva o por comprensión, describiendo una condición que cumplen sus elementos :
- A es el conjunto cuyos miembros son los números enteros positivos menores que 5.
- B es el conjunto de colores de la bandera de México.
La segunda manera es por extensión, esto es, listando cada miembro del conjunto. En una definición extensiva se escriben los elementos del conjuntos entre llaves:
- C = {4, 2, 3, 1}
- D = {blanco, rojo, verde}
Puesto que un conjunto queda especificado únicamente por sus elementos, a menudo pueden usarse ambas definiciones, intensivas y extensivas, para especificar un mismo conjunto. Por ejemplo:
- «El conjunto de las vocales en español» = {e, u, a, i, o}
- En los ejemplos anteriores, se tiene que A = C y B = D
Debido a la propiedad de la extensionalidad, el orden en el que se especifiquen los elementos de un conjunto es irrelevante (a diferencia de una tupla o una sucesión). Por ejemplo:
- C′ = {1, 2, 4, 3} es igual a C = {4, 2, 3, 1}
- D′ = {verde, blanco, rojo} es igual a D = {blanco, rojo, verde}
Esto es así debido a que lo único que define un conjunto son sus elementos. Por ejemplo, cada elemento de D es un elemento de D′ y viceversa, luego ambos son necesariamente el mismo conjunto. Del mismo modo, y a diferencia de un multiconjunto, cada elemento de un conjunto es único: no puede repetirse o pertenecer «más de una vez». Esto significa que, por ejemplo:
- {4, 3, 2, 4} = {4, 2, 3} ,
ya que los elementos de ambos conjuntos son los mismos: el 4, el 3 y el 2. No sería el caso si los números que consideramos tuvieran alguna otra propiedad que los diferenciase:
- {4, 3, 2, 4} es distinto de {4, 2, 3} y de {4, 2, 3}
Es habitual utilizar las llaves también en las definiciones intensivas, especificando la propiedad que define al conjunto:
- {Vocales del español} = {o, u, i, e, a}
- {Palos de la baraja francesa} = {♠, ♣, ♥, ♦}
Otra notación habitual para denotar por comprensión es:
- A = {m : m es un entero, y 1 ≤ m ≤ 5}
- B = {c : c es un color de la bandera de México}
- F = {n2 : n es un entero y 1 ≤ n ≤ 10} ,
donde en esta expresión los dos puntos («:») significan «tal que». Así, el conjunto F anterior es el conjunto de «los números de la forma n2 tal que n es un número natural entre 1 y 10 (ambos inclusive)», o sea, el conjunto de los diez primeros cuadrados de números naturales, {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}. En lugar de los dos puntos se utiliza también la barra vertical («|») u oblicua «/» .
[editar]Pertenencia
La relación clave en un conjunto es la pertenencia: cuándo es un elemento miembro de un conjunto. Si a es un miembro de B, se denota por a ∈ B,4 y si no lo es, se denota por a∉ B. Por ejemplo, respecto a los conjuntos A, B y F de la sección anterior, podemos decir:
- 4 ∈ A , 36 ∈ F , verde ∈ B , pero
- 7 ∉ A , 8 ∉ F , azul ∉ B
Y se dice entonces que 4 pertenece al conjunto A, 4 es un miembro de A, 4 está en A o A contiene 4.
[editar]Subconjuntos
|
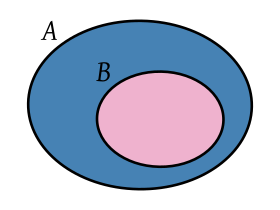
Esta definición es equivalente a: «si todo elemento de un conjunto B pertenece también a otro conjunto A se dice que B esta contenido en A, o bien que B esta incluido en A. Esta idea se indica con el signo ⊂ y se lee 'esta contenido en'».8
|
Si B es un subconjunto de A, se escribe como B ⊂ A y se dice que «B está contenido en A». También puede escribirse A ⊃ B, y decirse que A es un superconjunto de B y también «A contiene a B» o «A incluye a B».
[editar]Subconjunto propio e impropios
En algunos textos de redacción antigua diferencian entre los subconjuntos: los subconjuntos, los subconjuntos propios y los impropios, esta notación no es aconsejable al ser obsoleta, dado que las estructuras algebraicas de orden y en álgebra de conjuntos, parten de la propiedad reflexiva, por eso un conjunto cualesquiera se considera un subconjunto de si mismo en todos los casos,9 y por ello se define:
|
|
|
Si B no sólo contiene algunos sino todos los elementos A, B no sólo es un subconjunto de A, sino que ambos conjuntos son iguales, A = B. El otro caso posible es que B contenga algunos pero no todos los elementos de A: B es un subconjunto de A pero no son iguales. Se dice entonces que B es un subconjunto propio de A y se denota B ⊊ A, es decir: B ⊆ A pero B ≠ A (y equivalentemente, para un superconjunto propio, A ⊋ B).
También se utiliza la notación B ⊂ A y A ⊃ B, pero según el autor esto puede denotar subconjunto, B ⊆ A y A ⊇ B; o subconjunto propio, B ⊊ A y A ⊋ B.10
Ejemplos.
- El «conjunto de todos los hombres» es un subconjunto propio del «conjunto de todas las personas».
- {1, 3} ⊊ {1, 2, 3, 4}
- {1, 2, 3, 4} ⊆ {1, 2, 3, 4}
[editar]Conjuntos disjuntos
Un conjunto A es disjunto a otro B si los elementos de A no pertenecen a B:
la disjunción de conjuntos es reciproca y si A es disjunto de B, B es disjunto de A:
Por lo tanto dos conjuntos A y B son disjuntos si no tienen elementos comunes, que también puede decirse:
|








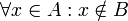


No hay comentarios:
Publicar un comentario